Autor: Aleksandra Arkit
Według słownika PWN, aproksymacja to ujęcie czegoś w sposób niezupełnie ścisły lub zastąpienie jednych wielkości matematycznych przez inne, przybliżone, mające na celu rozwiązanie pewnego problemu, którego nie da się przedstawić dokładnie w postaci analitycznej.
Jest to podejście często wykorzystywane w modelowaniu matematycznym czy w metodach numerycznych. Również w życiu codziennym mamy do czynienia z aproksymacją, gdy nie możemy być do końca precyzyjni – na przykład podając szacunkowy koszt wykonania usługi, podczas, gdy jej rzeczywisty koszt będzie ostatecznie powiązany z faktycznie zużytymi materiałami czy czasem trwania wykonania usługi. Planując podróż lub idąc na zakupy również dokonujemy szacunku kosztów, dobierając produkty w taki sposób, aby ich łączna cena nie przekroczyła założonego budżetu.
W ideę aproksymacji wpisuje się znana wszystkim liczba pi, gdyż nie jesteśmy w stanie podać jej dokładnej wartości i często posługujemy się jej przybliżeniem: 3.14.
Jest to na tyle ciekawe zagadnienie, że warto włączyć je w proces dydaktyczny mając na celu realizację podstawy programowej w zakresie sprawnego wykorzystywania narzędzi matematyki w życiu codziennym, a także kształcenie myślenia matematycznego ukierunkowanego na kreatywne rozwiązywanie problemów z różnych dziedzin ze świadomym wykorzystaniem metod i narzędzi wywodzących się z informatyki.
W celu ujarzmienia i oswojenia liczby pi proponujemy ćwiczenie w celu oszacowania jej wielkości.
W pierwszej kolejności prosimy uczniów o zapoznanie się z apletem dynamicznym LICZBA PI, a następnie rozpoczynamy dyskusję na temat jego merytorycznej zawartości.
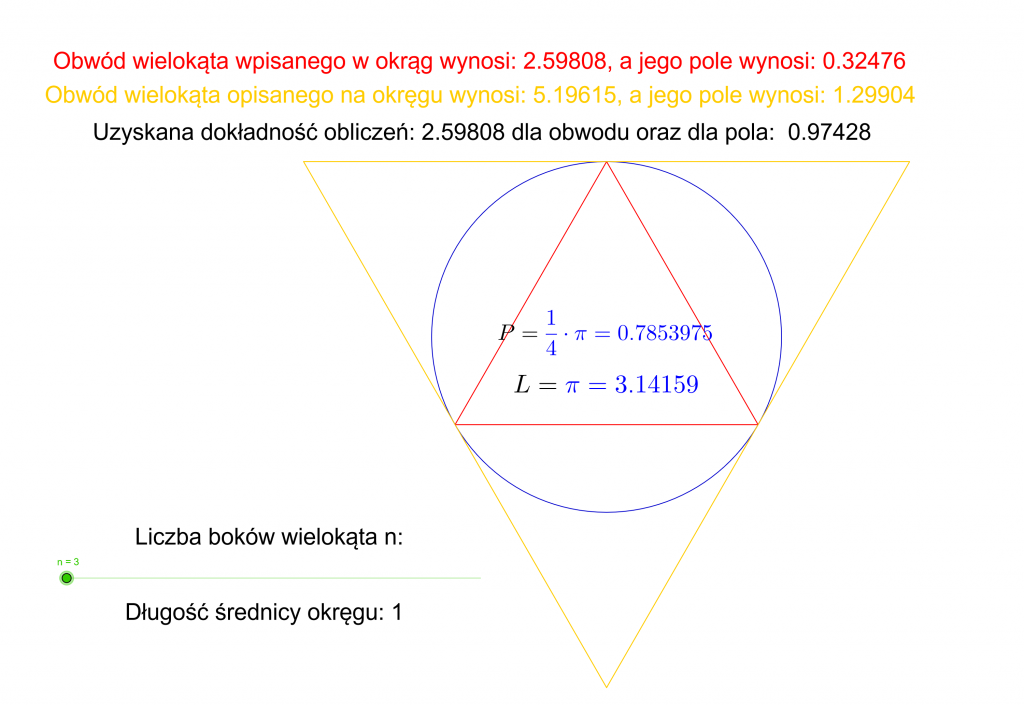
Liczymy na „odkrycie” reguły, że im więcej boków ma wielokąt foremny opisany lub wpisany w okrąg o średnicy równej 1 jednostce, tym bliższa jest wartość jego obwodu długości okręgu równej pi. Następnie proponujemy sprawdzenie tej reguły przez wyznaczenie obwodów odpowiednich wielokątów dla różnej liczby boków. Każdej grupie przydzielamy inną liczbę boków wielokątów foremnych. Prosimy o porównanie otrzymanego wyniku z wartością prezentowaną w aplecie dla odpowiedniej liczby boków i wyznaczenia błędu względnego przyjęcia długości obwodu wielokąta do oszacowania liczby wartości pi. Uzyskane wyniki przez poszczególne grupy możemy przedstawić w postaci ciągu liczbowego i zilustrować jego wyrazy na wykresie. W przypadku realizacji programu matematyki na poziomie rozszerzonym określamy ten ciąg wzorem ogólnym i obliczamy jego granicę w celu potwierdzenia prawdziwości zaobserwowanej reguły. Analogiczne rozumowanie można przeprowadzić dla pola koła, ale warto wtedy do obliczeń przyjąć średnicę koła równą dwóm jednostkom.
Celem tego ćwiczenia jest wprowadzenie uczniów w świat modelowania matematycznego, przybliżenie pojęcia aproksymacji, jak również zmierzenie się z wymaganiami ogólnymi kształcenia matematycznego podstawy programowej w zakresie rozumowania i argumentacji oraz wymaganiami szczegółowymi w zakresie stosowania twierdzenia kosinusów, rozwiązywania trójkątów czy obliczania pola trójkąta o danym kącie. Wartościowe jest również przedstawienie wyników w postaci ciągu liczbowego i analiza jego własności w kontekście wymagań ogólnych kształcenia matematycznego podstawy programowej w zakresie wykorzystania i interpretowania reprezentacji.





